This is a simple algorithm, but there is more to it than just finding k. Hyperparameters include:
- n_neighbors or k: the number of nearest neighbors to use for each prediction. We consider the space [1, 1000].
- weights: whether to weigh the more distant of the k points less. The options are {uniform, distance}.
- metric: the distance metric to use for the tree. We’ll stick with the default “minkowski,” which provides some flexibility: (\sum |x - y|^p)^{1/p}
- p: the power parameter for the Minkowski metric. This would only affect distance-based weighting. The value 1 equates to the Manhattan distance, and 2 equates to the Euclidean distance. We consider three values in the hyperparameter search: {1, 2, 3}.
- algorithm: the algorithm for finding the nearest neighbors. We use with “kd_tree” because it supposed be the most appropriate algorithm for low-dimensional problems.
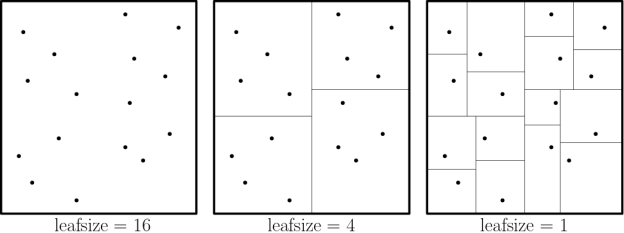
- leaf_size: this is the number of points at which to switch to brute-force search for nearest neighbors. It affects both search speed and memory requirements, but not the search results. We set it to 2000.
Experiment Design
For our tests on univariate smooth, we use:
- sklearn.neighbors.KNeighborsRegressor for the modeling
- skopt.forest_minimize to optimize the hyperparameters
We run the hyperparameter optimization routine with 50 calls to an objective function, which itself uses 3-fold cross-validation. We run the hyperparameter optimization routine 25 times on new synthetic datasets, with the datasets in groups growing in size by powers of 2.
Results
The results are poor.
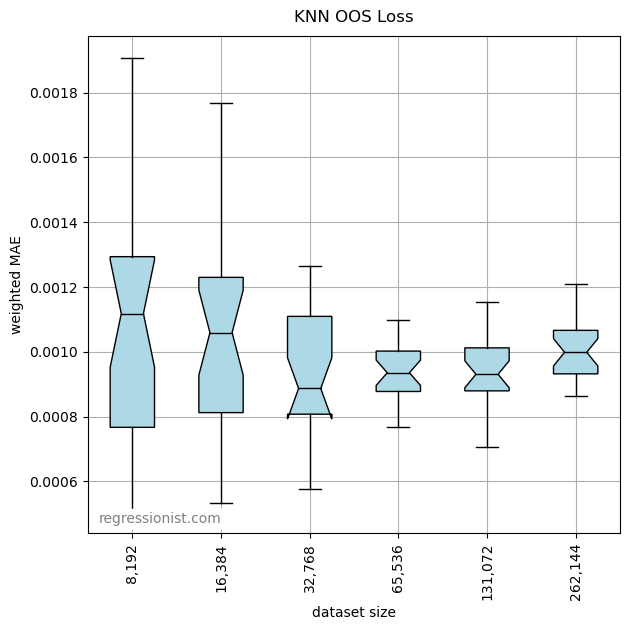
KNN scales terribly, both in time and memory requirements. Even when using the KD Tree algorithm to simplify the search for nearest neighbors. So, we were unable to test larger synthetic datasets.
Even on these small datasets, the hyperparameter optimizer chose a large number for k, averaging 867. The optimal value for k would logically increase with the size of the dataset. That would exacerbate the scalability issues.
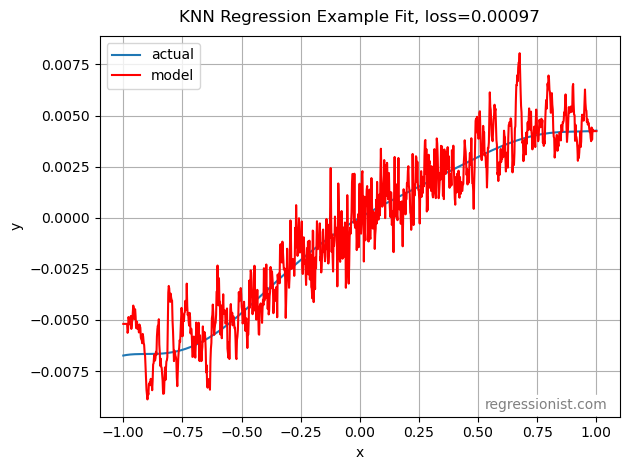
Here is an example fit from the largest dataset size tested:
Conclusion
This isn’t the method you’re looking for. It just doesn’t scale.