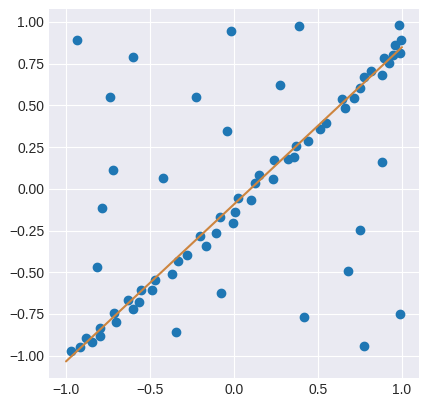
The Random Sample Consesus (RANSAC) algorithm performs linear regression by separating sample data from the input into inliers and outliers. It then creates a model that is estimated only from the inliers and remains unaffected by the data classified as outliers. The algorithm works by the doing following:

1. Select random samples from the training data and create a linear model for this subset.
2. Divide datapoints in the entire dataset into inliers and outliers using a user-provided residual threshold and calculate the model score.
3. Repeat either a maximum number of times or until a certain number of inliers is reached (both parameters provided by the user). If the model of one iteration has a greater number of inliers than that of the previous, it replaces it as the best model.

A final model is then made based on the inliers of the best model obtained by the algorithm.

Experiment Design

Here we test how the RANSAC algorithm performs on the univariate smooth dataset. We use the scikit-learn implementation of RANSAC for the actual algorithm and skopt.forest.minimize in our optimization.

For RANSAC, we optimize the following hyperparameters:

• min_samples: minimum number of samples to be taken from the original data. We draw uniformly from [10, \lfloor \frac{m}{2} \rfloor] where m is the dataset size.
• residual_threshold: maximum residual for a data sample to be classified as an inlier. We draw from a base 10 log-uniform distribution on the interval [0.0001,0.1].
• max_trials: maximum iterations for random sample selection with default as 100. We draw uniformly from [50,1000].

We perform the hyperparameter optimization process with 50 calls to an objective function that uses 3-fold cross-validation. We run the optimization routine 25 times on new synthetic datasets growing in size by 2,000 from 4,000 to 24,000.

Results

Here we observe the error for models made on increasing dataset sizes:

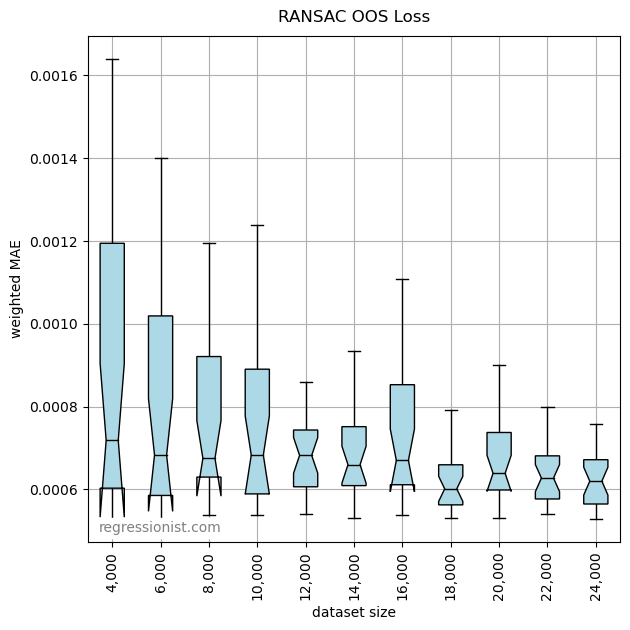
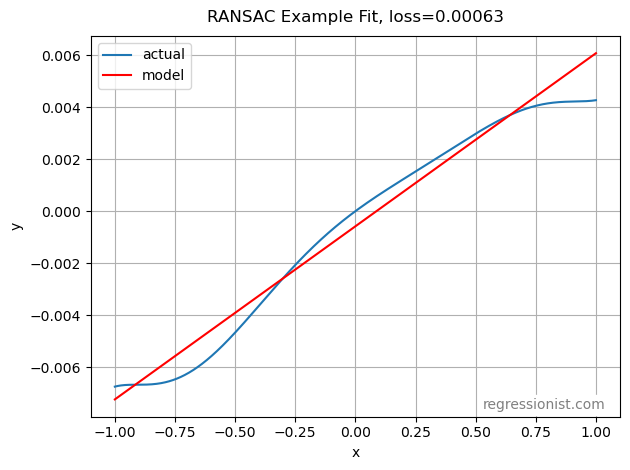
Although given enough data a non-linear model will eventually make a better fitting model than RANSAC ever can, because the RANSAC model is linear, it converges to a good model quickly, even with limited data. Here we see an example of the fit from our largest dataset:

Conclusion

During the optimization process, allowing a higher min_samples parameter helped the RANSAC algorithm create more consistent models. RANSAC is a good choice when data is very noisy and limited. As a linear model, it has some limitations when facing non-linear data, but it runs very quickly and handles noise well.